Kahneman 1979 - Prospect Theory - An Analysis of Decision Under Risk

Google Scholar Link

Kahneman, & Tversky, A. (1979). Prospect Theory: An Analysis of Decision under Risk. Econometrica, 47(2), 263–291. https://doi.org/10.2307/1914185

Summary

Expected utility theory, sometimes referred to as expected value, posits that preferences are stable and can be determined using the following equation -

\[\begin{aligned} \Large EV(x,p) &=\Large{ p \cdot x }\\ EV &=\text{expected value}\\ p &=\text{probability}\\ x &=\text{value} \end{aligned}\]

Whichever course of action results in the largest expected value will be selected. This is not always the case however. Preferences can be reversed (called the reflection effect) - as is the case in the trolley problem. Additionally, probabilities are frequently misconstrued, which affects decisions. To remedy these theories, prospect theory is introduced, which takes the Expected Value equation and introduces two functions into it.

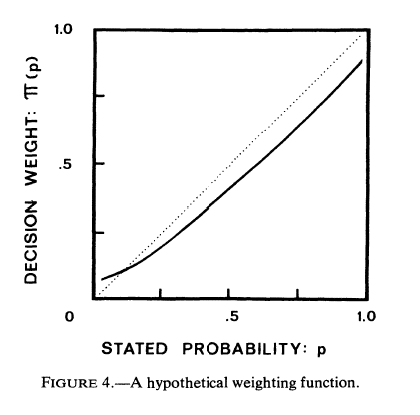
\[\begin{aligned} \Large EV(x,p) &=\Large{ \pi(p) \cdot v(x) }\\ EV &=\text{expected value}\\ p &=\text{probability}\\ \pi &=\text{the weighting function}\\ x&=\text{value}\\ v&=\text{the value function} \end{aligned}\]

The weighting function recognizes that lower frequencies are often subjectively over-estimated and higher frequencies are often subjectively under-estimated.

The function, which takes an objective probability as input and outputs a decision-weighted probability, is shown in the following diagram…

Note: Current research indicates that the actual crossover for true probability and decision-weighted probability occurs at approximately 0.35 (not the lower value shown on this graph).

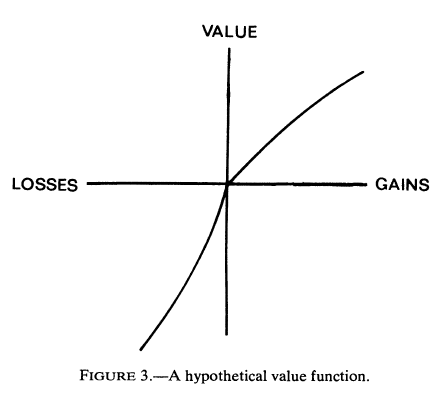
The value function highlights the fact that, rather than being sensitive to absolute magnitudes, humans are instead attuned to relative changes. As the authors put it, “The same level of wealth, for example, may imply abject poverty for one person and great riches for another – depending on their current assets.” Specifically, “losses loom larger than gains.” This is shown by the fact that the loss side of the function has a steeper slope than does the gain function. The value function is both monotonic and non-linear, as shown below…

Application

It’s important to be aware of how prospect theory affects our intuitive decision-making. In situations where we have something, and might lose it (negative framing), we act risk averse. In situations where we owe something, and might not have to pay it back (e.g., “double or nothing” - positive framing), we are risk-seeking.